Mathematical Notes About Neural Networks

Hello everybody,

today I want to write few words about topic why mathematician believe that neural networks can be taught of something. Recently I've read book Fundamentasl of Artifical Neural Networks of Mohamad Hassoun and want to share some thoughts in more digestible manner with omitting some theoretical material.

As you heard, when first attempt of neural networks was invented ( aka Perceptron), society was very admired by them, until Marvin Minsky and Seymour Papert showed that Perceptrons can't implement XOR function or in generally speaking any non linear function.

It lead to big disappointment in area of neural networks.

But why? Because sometime one line is not enough in order to approximate some kind of function. So what is needed in that case? The answer is simple, to add another line.

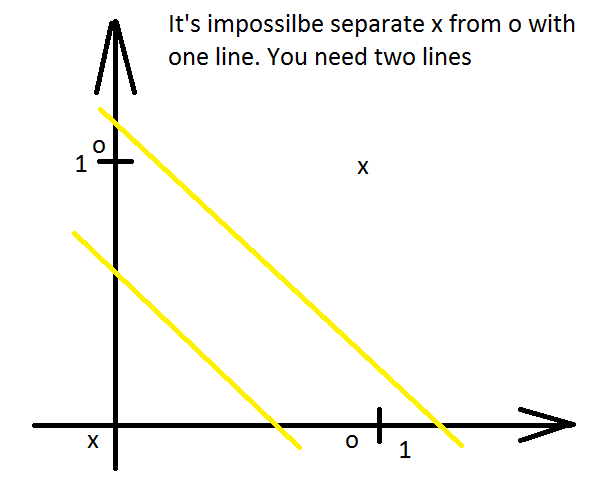
Then question raised who can give guarantee that it is possible with help only lines to solve separability problem? This kind of guarantee become Stone-Weierstrass. And what if you want to separate your area not with help of lines, but with help of some more complicated curves? Where to go for? Is it possible to make separability bo something else? You will be surprised, but yes, and this kind of guarantee was granted to all of you with help of Kolmogorov theorem. Of course both of them have some kind of limitations of what you can expect to approximate, but in general Kolmogorov and Stone-Weierstrass theorems say that it is possible to approximate some function through combination of other functions or even as combination of other simpler functions, if you need.

Inspired by the power of approximation and the potential of combining simpler elements to solve complex problems? Just as neural networks can be enhanced to achieve remarkable capabilities, your Acumatica system can be tailored to meet your unique business needs. Whether it's a custom feature, integration, or workflow optimization, our team is ready to bring your vision to life.

Leave a customization request today and let us help you unlock the full potential of your Acumatica platform. Together, we can build a solution that fits your business like a glove.