Coefficient Of Determination
Hello everybody,
Today I want to describe some ideas about measure quality of learning.
First of all I want to point areas where you can apply those measurements. It can be in three areas:
- For setting funtional during learning
- For picking hyperparameters
- For evaluation of ready made model
Another way can be combination. You can measure quality during learning with one measurement, but final model you can analyze with other measurement.
MSE
So, let's start with most common formula: mean squared error:
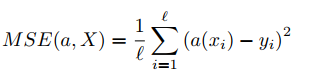
In words it reads the following: difference between prognozed value and desired value, squared, summed and finally averaged.
MSE has following featues:
- Easily minimizable
- Punishes stronger for bigger mistakes
What it means in practice? If your learning data set has many anomalies, then MSE is definetely not a point to apply. But if your data is without anomalies then MSE is really good choice. Because MSE will learn anomalies. And you don't want your model to learn anomalies, right?
MAE
Another point of choice for data scientists is mean averaged error:
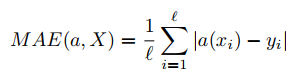
In words it is averaged module of difference between desired output and actual output.
It has following features:
- Harder to minimize
- Less punishes for bigger mistakes
In practice it means that if your learning set has plenty of anomalies then MAE is one of the functions to consider.
Coefficient of detemination
Means squared error has interesting modification, coefficient of determination. Take a look at formula:
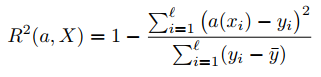
where 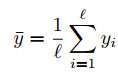 is average answer value
is average answer value
The main part of coefficient is fracition, in which numerator has sum of squared deviations, while denominator has sum of deviations of answers.
So, what coefficient of determination explains? It explains which part of dispersion is explained or modeled in whole dispersion of answers. It's value is also interpretable.
It has following features:
For workable models coefficient of detemrnation is between zero and 1.
If coefficient of detemrnation is equal to 1 then we built ideal model.
If coefficient of detemrnation is equal to zero, then model is like constant value
If coefficient of detemrnation is smaller then zero then model is worse then constant value.
Asymetric error
Consider following scenario. You are owner of shop that sells laptops. And you have following question mark for yourselves: what amount of laptops to preorder. Another question mark that you get is maybe it's better to have little bit more laptops then needed? For such a cases maybe you can consider stronger punishment for under forecast then over forecast. One of the example of functions that can be used is quantile error. Take a look at formula:
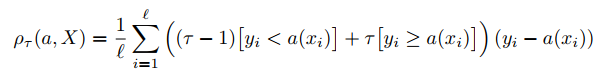
It looks pretty complicated, so let's go in some details of it.
Parameter τ ∈ [0, 1] defines for what to punish stronger: for over forecast or under forecast.
If τ is closer to 1 then model will be punished for under forecaset, otherwise for over forecast.
If this formula looks complicated below goes visual explanation:
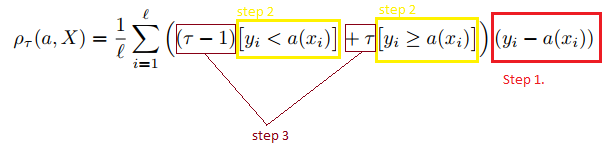
So,
step #1 calculate difference between desired output and model output
step #2 choose multiplier
step #3 in case of under forecast we multiply by τ - 1 and summ it. In case of over forecast multiply on τ.
Ready to take your Acumatica experience to the next level? Just as data scientists carefully choose the right metrics to optimize their models, your business deserves tailored customizations to maximize efficiency and performance. Whether you need a unique feature, a specific integration, or a workflow enhancement, our team is here to bring your vision to life.
Leave a customization request today and let us help you build the ideal solution for your business needs. Don’t settle for a one-size-fits-all approach—customize Acumatica to work perfectly for you!