Hello everybody,

today I continue writing notes about measuring quality of learning. You can read my previuos artcile 1 and article 2 about measures of quality of learning. If to summarize two of those articles we have the following:

1. accuracy is good measure, but if samplings is unbalanced then accuracy can have great numbers, but total model will be very bad.
2. precision tells you how objects model a(x) can find
3. precision and recall work fine on unbalanced samplings

And then question arises, is it possible somehow to merge them, but not as accuracy but as something more meaningful then accuracy?

I'll decribe different ways to describe it going from worsest to better and hopefully the best algorithm.

Average

Let's consider first example: average value of precision and recall. Take a look at the following formula:

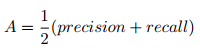
Take a look how possible chart can look like:

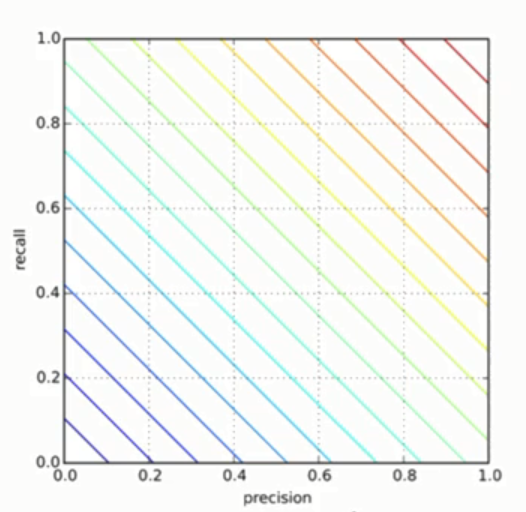
First of all you can see lines drawed with step 0.2 . That is because formula of precision is linear formula. 

consider following case. You've made a model that gives you following criteria

precision = 0.1

recall = 1

A = 0.5 * (1 + 0.1) = 0.55

In reality that can be constant output model, that always says 1 as response, and if you have biased selection set which is 99% with 1 and only 1% with -1. That model is useless, but on chart it will look like this:

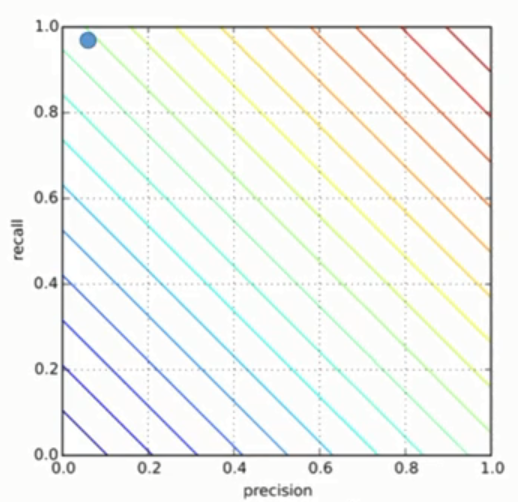
Consider another model:

precision 0.55

recall 0.55

A = 0.55

Combined picture will look like this:

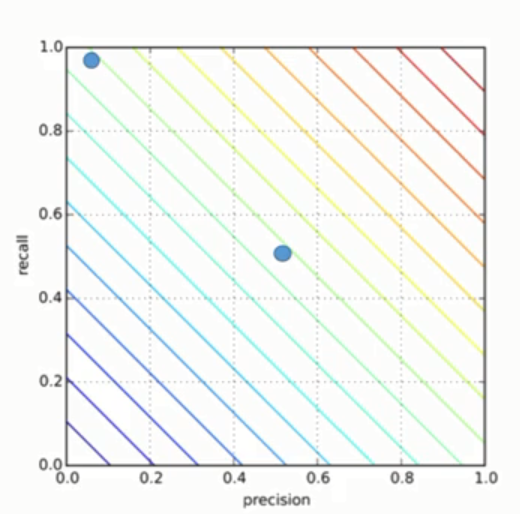
second model is much better then the first one, but both dots live on the same line giving idea that both of them are equally good. But in reality they are not. The second one is much better. Constant and good enough alrorithm receive the same measurement of quality. 

Minimum value

Ok, so let's throw away average value, and instead try optimization minimum value. Like in this forumla:

M = min(precision, recall)

Then just empty chart will look like this:

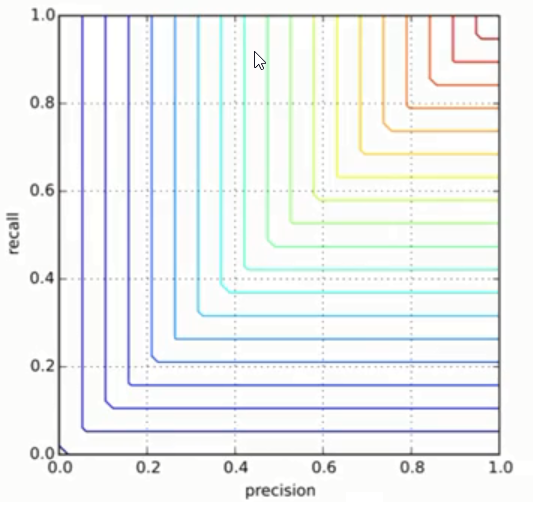
as you can see on the picture, good algorithms will be concentrated in top right corner. And the worse algorithms will be closer to left bottom part. 

But still it doesn't perform as well as we would like to. Consider two algorithms:

1.1.  precision 0.4

1.2. recall 0.5

1.3. M = 0.4

second one:

2.1. precision = 0.4

2.2. recall = 0.9

2.3. M = 0.4

They will look on chart like this:

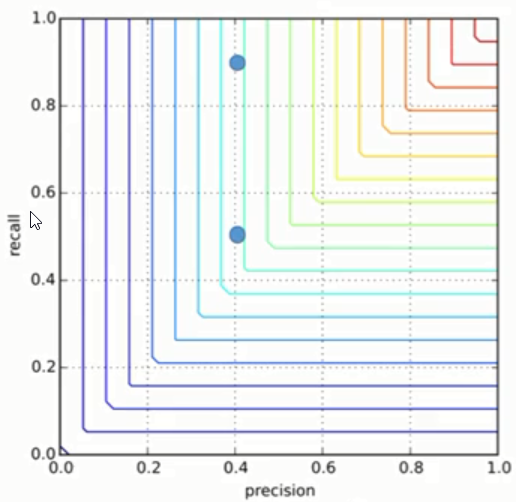
so, it is clear that second alorithm is better because with the same precision it gives higher recall. But on chart it is located at lover place, closer to bottom. Also both algorithms lie on the same linve, while in reality it shoudn't be the case. 

F-Measure

One more idea can be to smooth those lines with help of garmonic average, which is also named F-Measure. It has following formula:

Quite often β is assigned value 1. In that case F-measure look like this:

β plays a role of weight for precision ( in other words importance of precision ).

Consider two algorithms:

first:

1. precision = 0.4
2. recall = 0.5
3. F = 0.44

second:

1. precision = 0.4
2. recall = 0.9
3. F = 0.55

and how they look at chart:

so you can see that second algorithm is closer to right top corner or closer to ideal classifier. 

Let's come back to this formula:

Imagine following scenario. If you want to give priority to precision, what should be value of β ? Something bigger then 1. For example 2. 

If you want to give priority to recall, then β should be smaller then 1. For example 0.5.