Hello everybody,

today I want to describe some simple models of neurons. Bet before I'll continue, just few words why to worry at all about simplification of neurons. The answer on question why is simple: simplification helps to understand bigger picture ( well not always ) and also allows to apply mathematics and make analogies to other familiar systems.

Now let's see models of "Idealized" neurons:

1. Linear neurons.  Output is sum of bias plus multiplication of multiplication of inputs with weights.

Here is how it's chart look like:

2. Binary threshold neurons. It has following stages of calculation:

• Compute a weighted sum of the inputs (1)
• Send out fixed size spike of activity if the (1) exceeds a threshold

Below goes graphical representation with case if threshold = 1

thre are tow equal ways to write equation for binary threshold neuron:

3. Rectified Linear Neurons

it has features of linear and non-linear neurons. Sometime such model is useful.

4. Sigmoid neurons. That one uses some kind of function ( typically logistic ). Another important detail kind of function should be easily derivative.

Below goes example of logistic neuron:

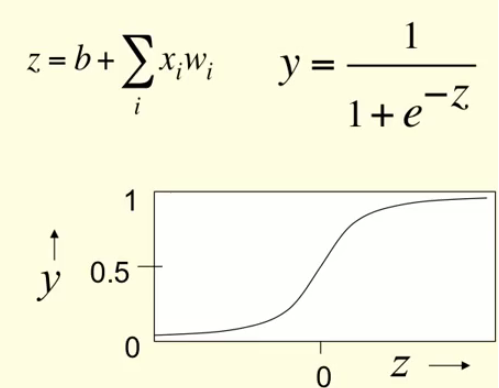
5. Stochastic binary neurons. For me it is puzzling. The use the same equation as logistic but they will output zero or one. And you never know for sure, what it will be. You just know, that the higher is output, the more chances of one, the lower is output, the more chances of zero.