Hello everybody,

today I want to share with you some ideas about activation functions in neural networks. 

But before I'll do this let's see simplified edition of neuron:

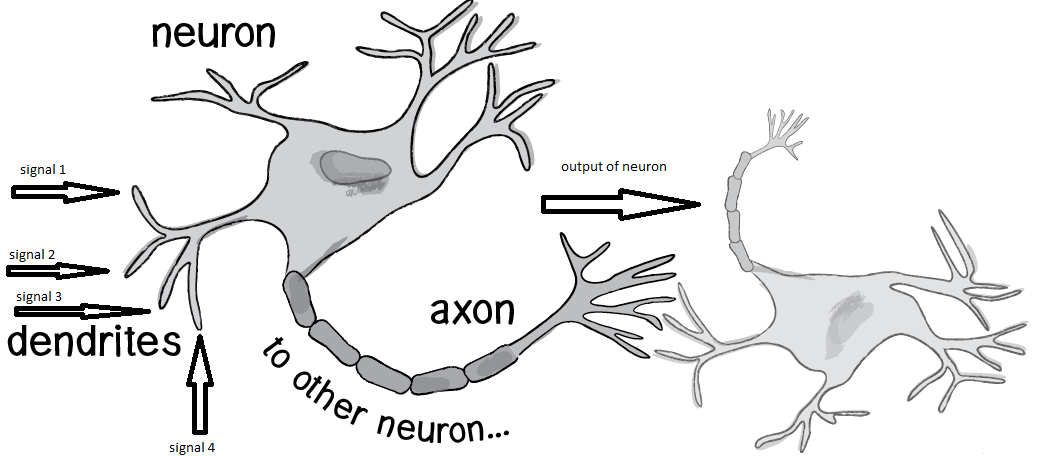
As usually many books describe following schema of working neuron:

ignals go into dendrites into neuron body. Neuron body does some kind of converting signal into another signal and sends output through axon to another neuron.

What is origin of signals, or where they come from? It can be any place of your body. It can be your eyes, it can be your nose, it can be touching of your hand, etc. Anything 

that your body signals is processed in the brain. 

So now, imagine, that you are mathematician and want to provide mathematical model of neuron? How you will represent it mathematically? One of the ways to implement it is following schema:

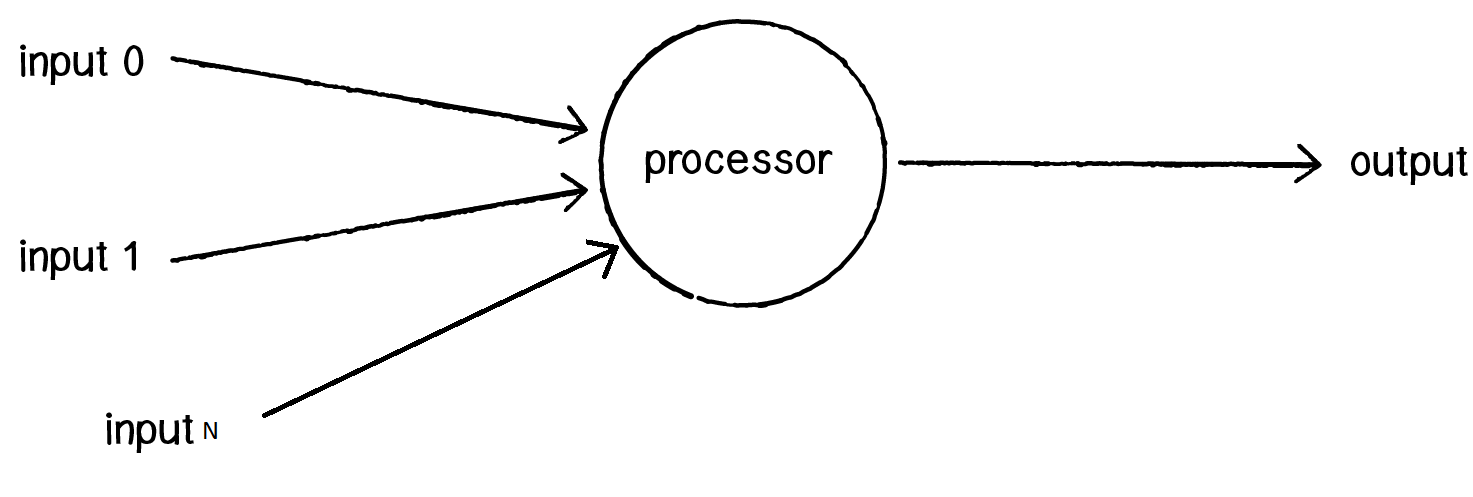
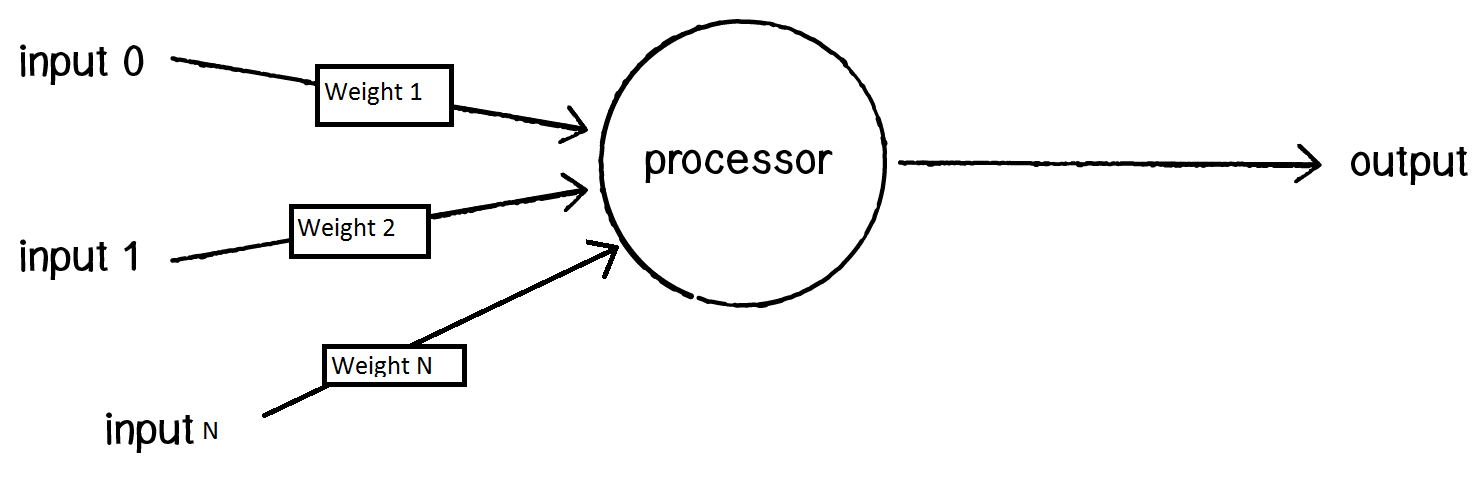
That is general picture of how neuron works. Just one more clarification is needed to say. Neuron not just takes input, but consider some inputs more important then another. Among neural networks developers

it is common practice to measure importance of some input as multiplier, which is named weight.

Take look at clarified mathematical model:

In your life it can looks like this. You want to get something like tasty lunch. And let's say you have no idea which proportions of bread and butter to use. What will you do? You will make experiment. Take piece of bread and put on it some small amount of butter. Try to taste it, and if you like it, you will stop adding butter. If you dislike it, you'll add more butter. And you'll continue adding butter untill you get sandwich that has enough butter and bread to make your lunch delicious. 

For this purpose you neuron will look like this:

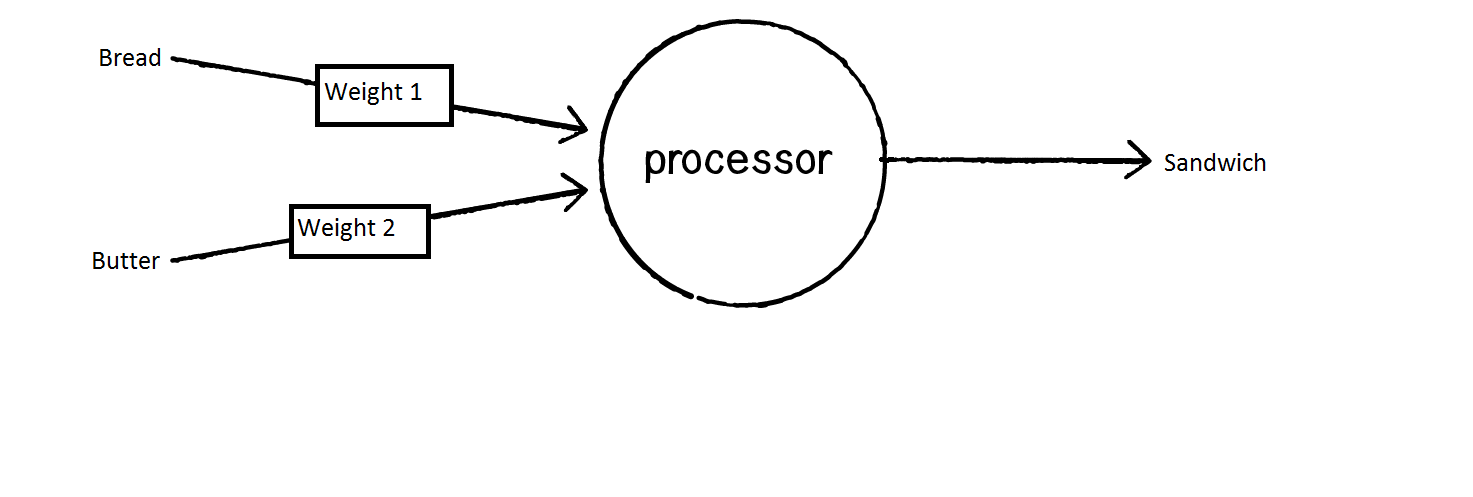
Pretty simple, huh? I can't tell for sure, but maybe in your had ther is a one neuron which remembers how much bread and how much butter you like.

Till know I didn't say what exactly processor does. To put simply processor can do the following:

1. Transfer furhter it's input. 

2. Modife input according to some rule and transfer it further.

What mean transfer input further? It means summ all values and send them to another neuron or command to your hand to put more butter or not. 

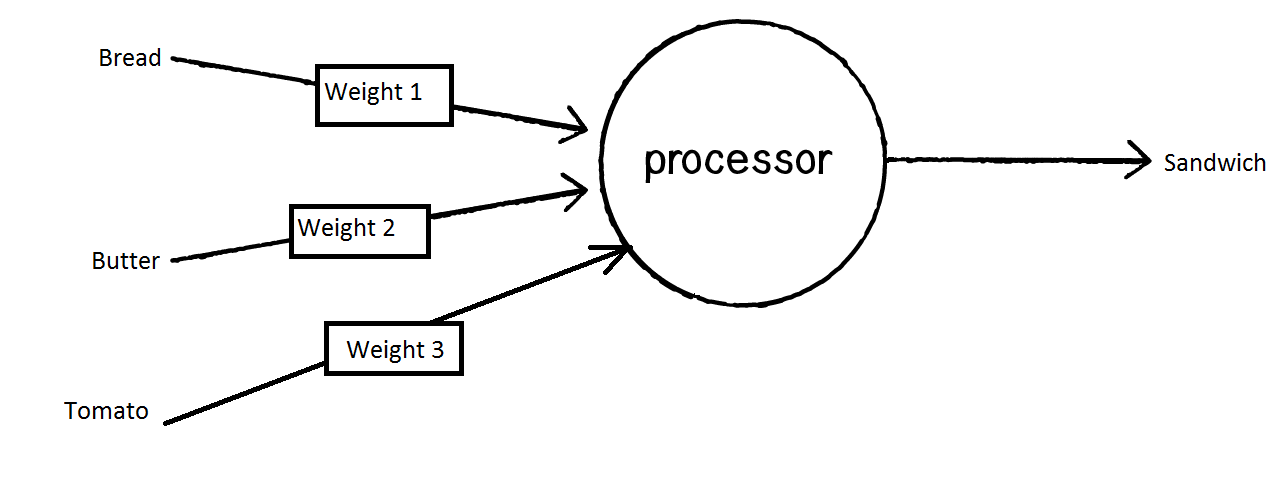
Before we consider second part let's try to give to our neuron task: figure out how much does it cost three different ingredients of your lunch. Let's say that your lunch consists of three ingredients:

bread, butter, tomato.

Neuron in that case look like this:

As a way of example in English you can hear statement like this: I put more weight on factor x and y, and then on factor z. And brains of people can work differently. As a way of illustration: neuron of one girl can pub big weight on rozes, while neuron of another girl can put more weight on chamomiles, and neuron of another girl can put more weight on chocolate or even tea. And task of boy is to find which weight is biggest. Then find second biggest weight and third, and then boy can start new stage of his life. Sometimes happen another change in life. Due to some reasons weights in neurons can change. And if somebody likes chocolate it will not always be the case. If somebody feels nice smell of his ( her ) favorite dish weight of chocolate can become smaller, and person decides to eat something. And after eating weight of chocolate can be restored again to pre-eating state. 

Imagine, that for few times you've bought sandwich with bread, butter and tomatos, but different amounts of it. Assume, that you bought bread, butter and tomato three times, and payed according to following table:

In this table first row means, that you bought one portion of bread, two portions of butter, and three portions of tomato. And you payed for this 42 $

Next time you bought three portions of bread, two portions of butter and one portion of tomato and so on.

How you can find how much does it cost each portion of bread, butter and tomato? One of the ways is to solve system of equations. But one neuron can't solve system of equations. All what it can do, is change weight which is multiplied on signal.

In the first case, signals where 1, 2, 3. In the second case signals where 3, 2, 1. In the third signals where 5, 6, 7.

Your neuron can behave in the following way:

1. Suppose that each one portion of tomato, butter and bread costs 15$.

2. If each portion costs 15$, than total value should be 1 * 15 + 2 * 15 + 3 * 15 = 15 + 30 + 45 = 90.

3. 90 is to much. Almost double value

4. Calculate error: Error = 90 - 42 = 48

5. Proportionally to size of portion decrease weight of portion.

6. As we have three inputs, we should divide 48/3 = 16.

7. New assumed values for each portion should be the following: sum of each portion is 6 ( sum of all elements of first cell in first row, or 1 + 2 + 3 )

8. We need to decrease the first weight value on 2.6 (16 / 3 * 1)

9. Decrease the second weight value on 5.3

10. Decrease the third weight on 7.8.

11. It gives us new values of weights: 12.4, 9.7, 7.2

And so on. If to continue this process, sonner or later you will have some approximation of how much costs bread butter and tomato in some error range.

If to draw comparison with real life, it can be compared to case, if you need to hit at something at three places in order it to be opened. 

And if to summarize what processor does, processor works as adder machine. Is it fine or some kind of silver bullet which feets to all live cases? Not always.

Consider the case. Sometime shops have the following price policy: if you buy more then three tomatos, then you'll get some kind of discount. 

Another case in shop can be if you have multiple discount for tomato, bread and butter. In that case linear function definetely will not feet.

But which functions can feet? 

You can try to consider following functions:

  a. Logistic sigmoid

Here is the formula:

And here goes sample of chart:

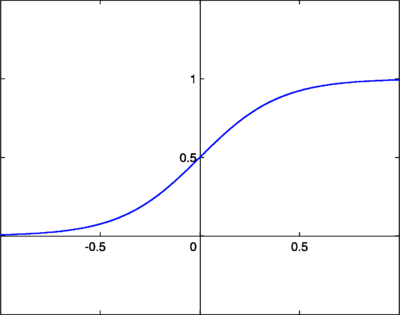
initially it become the most popular function in area of neural networks, but for now it become less popular. My personal preference is avoidance of it because it has small range (0;1)

  b. hyperbolic tangent

Formula:

tanh(x) = sinh(x)/cosh(z)

and chart:

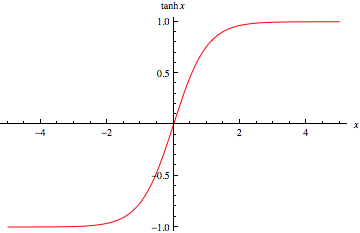
for now this is my favorite function which I use in my neural networks areas. Just want to clarify what I mean when I say favorite, I mean I start from this function and if not satisfied with output I can move to another activation functions.

  c. Heaviside step

formula:

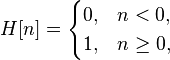
and image itself:

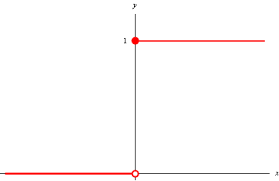
Functions like heaviside step as usually are good for classification tasks. 

Of course it is absolutely not complete list of activation functions for neural networks. Other activation functions are: Guassian, arctan, rectified linear function, SoftPlus, bent identity, etc.

So, if to summarize neuron architecture, it is summarizer with some kind of Activation function transformation. And you can try if you wish to make experiments with activation function which best feets to your needs.